PyProcar#
Pre- and Post- processing of Density Functional Theory Codes
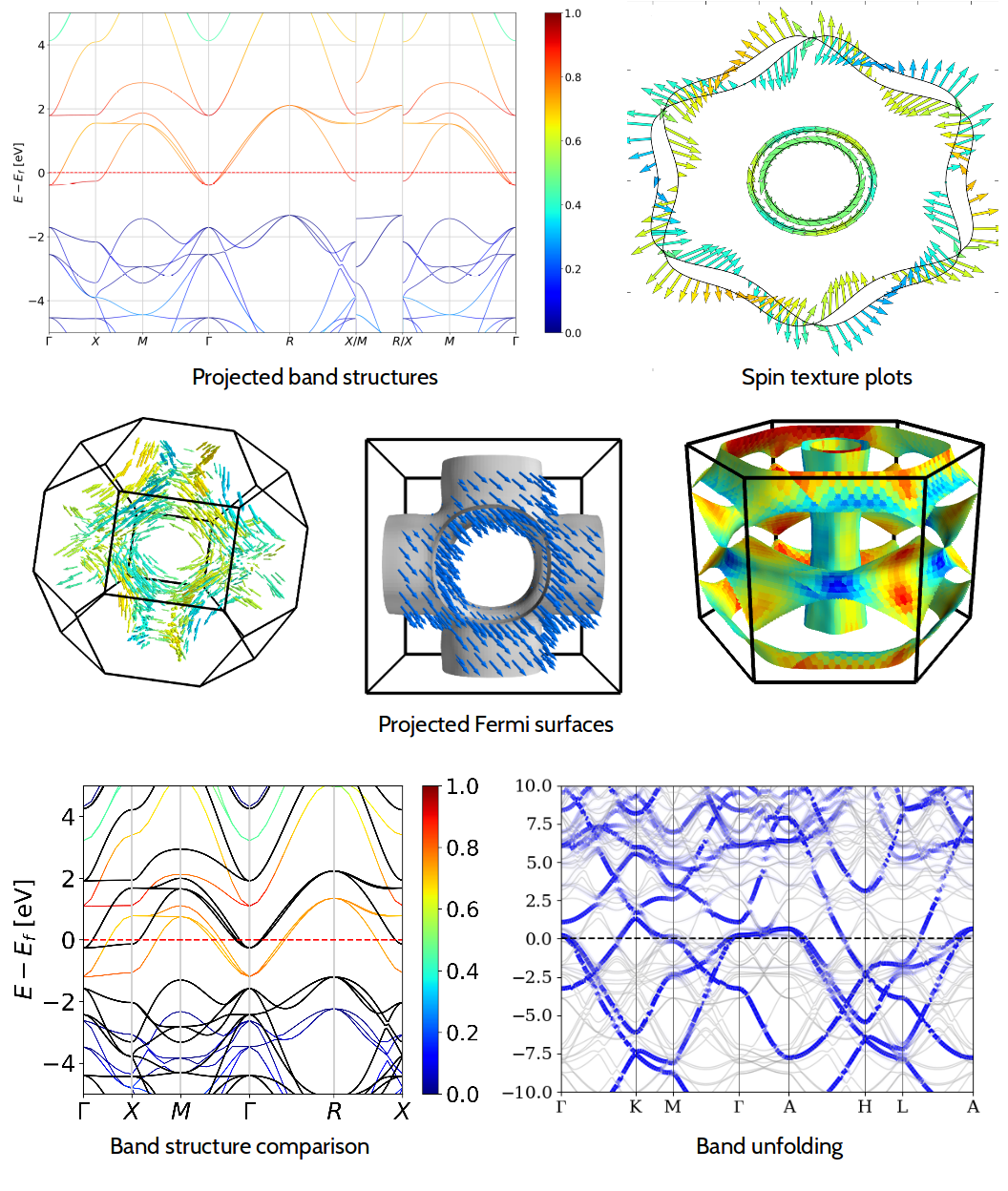
PyProcar is a robust, open-source Python library used for pre- and post-processing of the electronic structure data coming from DFT calculations. PyProcar provides a set of functions that manage data from the PROCAR format obtained from various DFT codes. Basically, the PROCAR file is a projection of the Kohn-Sham states over atomic orbitals. That projection is performed to every \(k\)-point in the considered mesh, every energy band and every atom. PyProcar is capable of performing a multitude of tasks including plotting plain and spin/atom/orbital projected band structures and Fermi surfaces- both in 2D and 3D, Fermi velocity plots, unfolding bands of a super cell, comparing band structures from multiple DFT calculations, plotting partial density of states and generating a \(k\)-path for a given crystal structure.
Currently supports:
VASP
Quantum Espresso
Abinit
Elk (Band Structure and Fermi in development)
Lobster (Stll in development)